"E' possibile che la patologia matematica, ovverossia il caos, sia la salute? E che la salute matematica sia la malattia?" …… "Quando raggiungi un equilibrio in biologia, allora sei morto!" Mandel A.
Gli organismi viventi sono oscillatori non lineari, o meglio, sono sistemi non lineari che esibiscono in certe condizioni ambientali comportamenti oscillatori complessi. Per un sistema non lineare non vale il principio che la risposta alla somma di due o più stimolazioni sia uguale alla somma delle risposte a ciascuna delle due stimolazioni prese singolarmente. In altri termini, non vale che all'aumentare della intensità di una "causa" vi sia un aumento della intensità della risposta.
Un esempio delle conseguenze della non linearità sono i fenomeni apparentemente improvvisi e catastrofici come la comparsa di effetti collaterali più o meno gravi ai dosaggi usuali di un farmaco, oppure la morte cardiaca improvvisa, ecc.. La morte cardiaca improvvisa permette di notare che, anche in un sistema in cui tutte le sue sottoparti (in questo caso le cellule cardiache) funzionano normalmente, una alterazione dei meccanismi di accoppiamento tra queste può causare effetti catastrofici.
Il seguente brano tratto dal volume di Sach sull'emicrania illustra chiaramente questa situazione in relazione alle emicranie periodiche e parossistiche:
"non si era in presenza di una situazione di causa-effetto, ma piuttosto di un fenomeno di "provocazione": stimoli che altre volte sarebbero stati trascurati e privi di effetti ad un certo punto facevano insorgere gli attacchi. Eventi infinitesimali, di per sé privi di importanza, potevano scatenare gli attacchi, divenire critici, una volta che il sistema avesse raggiunto una certa "configurazione", un "punto singolare". In tal modo non vi è più una relazione lineare tra stimolo e risposta, e non possiamo parlare in termini di causa ed effetto."
Ary Goldberger dell'Harvard Medical School ed i suoi colleghi sono stati molto attivi nella applicazione delle geometria frattale all'interpretazione dei sistemi fisiologici (Goldberger A & West B Yale J of Biology & Med 1987, 1: 421-435; West B & Goldberger A American Scientist 1987, 75 (4): 354- 365; Goldberger A et al Experientia 1988, 44: 983-987), soprattutto in relazione al cosiddetto caos deterministico, che ha mostrato di dare spiegazioni migliori, rispetto ai modelli tradizionali, della morte cardiaca improvvisa, della divisione cellulare, dei cambiamenti improvvisi dei livelli ormonali, di alcuni eventi nervosi ed altri processi non lineari in molte forme di vita. Altri lavori e teorie, quali quelli di Ilya Prigogine ('Dissipative Structures'), David Bohm ('Implicate Order') e Rene Thom ('Catastrophe Theory') si riferiscono a processi e sistemi non lineari. Ciò ha stimolato lo sviluppo di un nuovo paradigma interpretativo nel campo delle scienze biologiche. Infatti il caos e le altre teorie non lineari mostramo che i processi altamente deterministici e lineari sono molto fragili nel mantenere la "salute" in un ampio range di condizioni, mentre i sistemi caotici possono funzionare efficacemente in un ampio range di condizini differenti, offrendo perciò adattabilità e flessibilità. Questa plasticità di funzione rende il sistema capace di far fronte alla imprevedibilità e alla variabilità dell'ambiente, offendo una adattabilità dinamica invece di una più vulnerabile e precisa omeostasi.
In questo contesto, lo psichiatra A. Mandel rifletteva :"E’ possibile che la patologia matematica, ovverossia il caos, sia la salute? E che la salute matematica sia la malattia?” …. Quando tu raggiungi un equilibrio in biologia, allora sei morto!” (Gleick J 'Chaos: Making a New Science' 1987).
La fisiologia classica asserisce che i sistemi in salute si autoregolano a ridurre la variabilità e a mantenere la costanza fisiologica. Questo è il concetto di omeostasi che permea la fisiologia classica. Contrariamente a tali concetti di omeostasi e di ordine, analizzando attentamente i fenomeni biologici, quali ad esempio il battito cardiaco, notiamo che essi fluttuano in maniera complessa, anche in condizioni di riposo del soggetto. Ciò mostra che i sistemi di regolazione biologici non sono lineari e che operano in condizioni lontane dall'equilibrio classicamente inteso (omeostasi) e che pertanto il mantenimento della costanza non è l'obiettivo del controllo fisiologico. Anzi, nei soggetti ad alto rischio di morte improvvisa (inclusi quelli per infarto cardiaco) l'organizzazione frattale e non lineare viene persa. Elucidare i meccanismi frattalici e non lineari conivolti nel controllo fisiologico e nei network di signaling è la sfida emergente.
La nonstazionarietà e la non linearità dei segnali generati dagli organismi viventi (vedi figura 1) mina gli approcci meccanicistici tradizionali basati sull'omeostasi e su metodi biostatici convenzionali. La teoria del caos deterministico offre possiblitià di migliori spiegazioni.
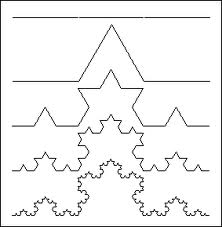
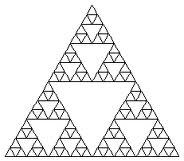
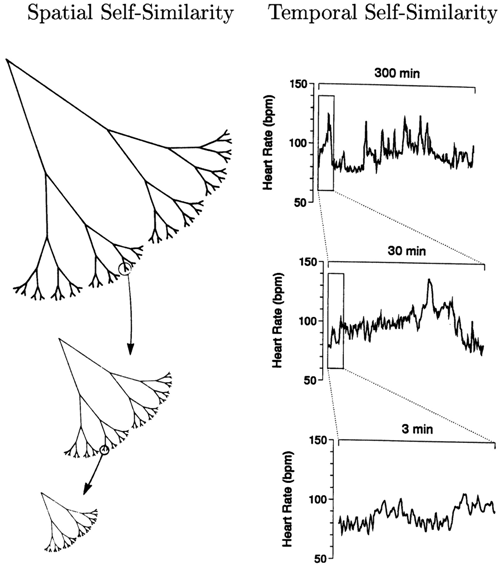
Il concetto di frattale, descritto da Benoit Mandelbrot nel 1975, si riferisce a oggetti geometrici irregolari che mostrano auto-somiglianza. Le forma frattaliche sono tutti quelle forme geometriche che non appartengono alle geometria euclidea di linee-piani-superfici, e che sono composte di subunità (e sub-subunità, e sub-subunità ecc.) ognuna somigliante all'intero oggetto (vedi fig. 2). Questa proprietà, detta autosomiglianza, si mantiene in tutte le scale dimensionali . Molte strutture non euclidee in natura, quali i rami di un albero, le coste, la superfici delle montagne sono frattaliche. Ed anche molte strutture anatomiche hanno una geometria frattalica, quali il sistema arterioso e venoso, l'albero tracheo-bronchiale, le ramificazione neuronali, la superficie interna del'intestino, il sistema di conduzione di His-Purkinje, ecc. Le geometria frattalica ed il concetto dell'autosomiglianza è un pò come il gioco delle scatole nelle scatole. Anche la struttura delle proteine, o più in generale il grado di irregolarità della loro superficie, è di tipo frattale e le dimensioni frattaliche variano con la regione della proteina esaminata. Similmente si è dimostrato che la sequenza della basi del DNA è di tipo frattale.
Come si può ben intuire gli oggetti frattali sono "irregolari" se paragonati agli oggetti regolari della geometria classica (euclidea), tuttavia hanno una forma riconoscibile. I frattali sono quindi oggetti regolarmente irregolari. Oggetti frattali sono i vortici (es. quelli del fumo di sigaretta, quelli della corrente di un ruscello): il loro aspetto globale è sempre riconoscibile, eppure non è mai eguale a se stesso. I frattali hanno anche un' altra proprietà: il grado di irregolarità rimane sempre lo stesso a qualsiasi scala di grandezza o temporale si osservi l'oggetto. Tale proprietà è detta autosomiglianza. Per dimensione frattale intendiamo, invece, la misura del grado di irregolarità di un oggetto.
Ovviamente ad avere una geometria frattale può essere un oggetto (frattale spaziale) o un evento temporale (frattale temporale).
Ovviamente una irregolarità spaziale o temporale potrà essere di origine casuale o di origine caotica. La differenza tra un fenomeno casuale ed un fenomeno caotico è nei gradi di libertà. Nel sistema casuale vi sono infiniti gradi libertà e ciò genera il comportamento casuale, nel sistema caotico i gradi di libertà sono finiti.
Quindi possiamo asserire che un fenomeno è casuale se la nostra incertezza, intesa come capacità predittiva, rimane immutata con lo scorrere del tempo. Ad esempio nel lancio di una monetina la nostra "stima" della provbabilitò di testa è la stessa sia che si tratti del prossimo lancio sia che si tratti del milionesimo lancio. Viceversa, in un processo caotico noi siamo in grado di prevedere con esattezza ciò che accade nell'immediato futuro, ma siamo sempre più incerti man mano che cerchiamo di prevedere quale sarà lo stato del sistema nel futuro. Tipico sistema caotico è la metereologia: una previsione nella scala dei giorni è relativamene affidabile, mentre diventa sempre più inaffidabile nel lungo periodo.
Da un punto di vista geometrico è possibile fornire una definizione operativa della differenza tra caso (rumore) e caos. Un traiettoria random si muove, per così dire, in tutte le direzioni dello spazio delle fasi, mentre una traiettoria caotica occupa una ben definita regione dello spazio.
Quindi il caso, essendo non deterministico, è impredicibile, mentre il caos, essendo deterministico, è impredicibile. Ovviamente avendo il caos una geometria spaziale e temporale complessa non è approcciabile con la geometria classica deterministica (quale quella newtoniana, che è applicabile ai sistemi lineari), ma con una geometria probabilistica (detta ergodica), basata su tecniche statistiche.
Sorge spontanea la domanda: si tratta di speculazioni epistemologiche, di mere curiosità matematiche, oppure questi strani risultati hanno importanti conseguenze in medicina?
La scoperta dei fenomeni caotici deterministici ha avuto una profonda ripercussione su concetti fondamentali, come ad esempio quello di normalità. La concezione più diffusa è che la normalità coincide cona la omeostasi, la stabilità, l'equilibrio. Di ciò abbiamo estesamente parlato in "metafore e linguaggio scientifico".
La possibilità di registrare in modo continuo diverse variabili fisiologiche, ha condotto ad alcune osservazioni rivoluzionarie. Ad esempio attraverso l'analisi dell'Holter cardiaco si è messo in evidenza che l'intervallo temporale tra i batti cardiaci, misurato sull'ECG come intervalli R-R, non è costante, bensì è soggetto a variazioni apparentemente casuali negli individui normali. La cosa più sorpredente è che negli inndividui malati e nelle ore immediatamente precedenti la morte si verifica una diminuzione della variabilità dell'intervallo R-R. Più il battito cardiaco è regolare e più un individuo è malato. Infatti lo spettro di potenza dell'intervallo R-R in una persona normale, mostra una vasta gamma di componenti oscillatorie.
Fig.1
L'immagine sopra (tratta da Goldberg) rappresenta la registrazione di frequenze cardiache in soggetti sani e malati per un periodo di 30 minuti. Volontariamente non è stata associata a nessuna rappresentazione grafica la condizione del soggetto. Una di queste rappresentazioni appartiene ad un soggetto in salute, le altre tre a soggetti con patologie. Siete capaci di identificare il soggetto in salute, quello cosidetto "normale"?
A e C sono tracciati ECG di pazienti con ritmo sinusale con severa insufficienza cardiaca. D è il tracciato di un soggetto con aritmia cardiaca, precisamente fibrillazione atriale, la quale produce un ritmo erratico della frequenza cardiaca. Il soggetto in salute è B, che è molto lontano dallo stato costante omeostatico che ci aspetteremmo stando alla fisiologia classica. Anzi esso è visibilmente nonstazionario e "irregolare", propretà tipiche dei frattali e dei sistemi non lineari. La perdita di questo caos si associa all'insorgenza di una eccessiva regolarià, di una periodicità (A e C) oppure di una perfetta casualità (randomness) priva di correlazioni. In C possiamo notare la presenza di oscillazioni fortemente periodiche (≈1/min), che sono associate ad un respiro di Cheyne-Stokes, un pattern respiratorio ciclico patologico.
Le rappresentazioni in figura 1 sollevano due importanti considerazioni:
– gli outputs dei sistemi in salute mostrano una complessa variabilità associata a correlazioni a lungo termine (frattaliche), insieme ad altre classi distinte di interazioni non lineari
– la complessità non lineare e multidimensionale tipica dei soggetti sani sembra diminuire o scomparire con l'invecchiamentio e la malattia, riducendo la capacità adattativa dell'individuo. Inoltre, questa perdita di frattalità e di non linearità possono essere quantificate con potenziali applicazioni diagnostiche e prognostiche.
Questa osservazionbe ha aperto nuovi scenari. Improvvisamente quella regolarità che era il presupposto stesso della idea della salute e della normalità come stabilità è stata messa in crisi: la malattia diventa una perdita di irregolarità, o se si vuole di complessità e la salute uno stato regolare di irregolarità.
Lo stesso processo di invecchiamento viene concepito, ora, come una perdita di gradi di libertà o, come un aumento di regolarità. Ad esempio l'elettroencefalogramma dei sogegtti anziani è caratterizzato da una perdita delle oscillazione di basso voltaggio e alta frequenza.
Lo stesso accade nella sclerosi multipla quando si osserva una EEG. Anche negli schizofrenici c'è una regolarizzazione del tracciato dell'EEG.
Nella figura sosprastante sono rappresentate strutture auto-somiglianti (self-similar) e fluttuazioni auto-somiglianti. Il simil-albero (sulla sinistra), un frattale spaziale, ha arborizzazioni auto-somiglianti, tale che la struttura in piccola scala assomiglia alla struttura in larga scala. Un processo frattale temporale, quale la regolazine di un cuore in salute (sulla destra) può generare fluttuazioni in scale di tempo differenti che sono statisticamente auto-somiglianti. Sulla destra infatti sono mostrate le frequenza cardiache di uno stesso soggetto su 3 scale di tempo differenti. Le tre rappresentazioni anche se appartenenti a scale di tempo differente sono molto simili, tanto da non essere statisticamente diverse: concetto di autosomiglianza frattalica. Una più rigorosa rappresentazione della autosomiglianza temporale della frequenza cardiaca di un cuore in salute è realizzabile con l'analisi wavelet (analisi della piccole onde), come nella figura sottostante
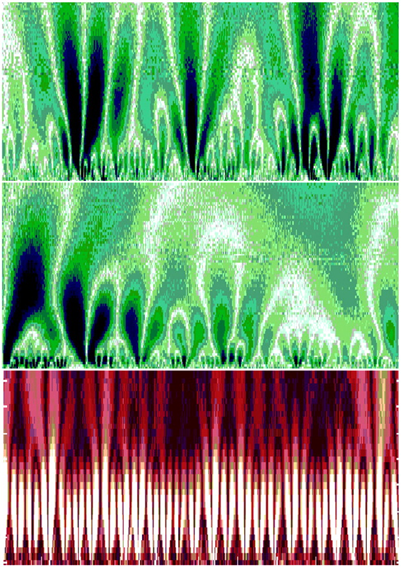
Color-coded wavelet analysis of a heart rate time series in health. The x axis represents time (≈1700 beats), and the y axis indicates the wavelet scale, extending from about 5 to 300 s, with large time scales at the top. The brighter colors indicate larger values of the wavelet amplitudes, corresponding to large heartbeat fluctuations. White tracks represent the wavelet transform maxima lines—the structure of these maxima lines shows the evolution of the heartbeat fluctuations with scale and time. This wavelet decomposition reveals a tree-like, self-similar hierarchy to the healthy cardiac dynamics. (Middle) Magnification of the central portion of the top panel, with 200 beats on the x axis and wavelet scale corresponding to about 5 to 75 s on the y axis, shows similar branching patterns. (Bottom) In contrast, wavelet decomposition of heartbeat intervals (≈1500 beats) from a patient with obstructive sleep apnea, a common pathologic condition, shows the loss of complex, multiscale hierarchy, with emergent, single-scale (periodic) behavior. The wavelet scale (along the y axis) extends from about 5 to 200 s. The red background is used to provide contrast with the fractal cascades under healthy conditions, shown in the Upper panels.
La fondamentale caratteristica dei sistemi in salute è l'adattabilità, ovverossia la capacità di rispondere a stimoli e stress non predicibili. La plasticità funzionale richiede una ampio spettro di output integrati. La fisiologia frattale, esemplificata da correlazioni a lungo termine (long-range) nella frequenza cardiaca umana, ha migliori capacità adattative per almeno due buoni motivi:
– correlazioni long-range servono come meccanismo di auto-organizzazione per processi altamente complessi che generano fluttuazioni intorno ad un ampio spettro di scale temporali
– l'assenza di una una scala caratteristica inibisce l'emergenza di comportamenti altamente periodici, che diminuirebbero di molto la capacità di risposta funzionale del sistema. La irregolarità caratteristica di un individuo sano è la base per il suo dattamento: è come se la irregolarità fosse una spia della capacità dell'organismo di reagire in diverse direzioni. In questo senso la malattia corrisponderebbe ad una modificazione di uno o più parametri del sistema, tale da indurre la sotituzione di una comprotamento irregolare con un comportamento regolare. Lo stato di malattia può quindi essere considerato una perdita di complessità del sistema. E' stato così coniato il termine di "riserva spettrale", che è un indicatore dei gradi di libertà di risposta dell'organismo alle influenze ambientali, e la malattia è stata interpretata come perdita di riserva spettrale. Questa ultima congettura è supportata dai ritrovamenti che le condizioni morbose potenzialmente mortali, quali l'insufficiena cardiaca, sono accompagnate dalla pedtia di relazioni frattaliche e dall'insorgenza di un modo dominante (es. il respiro di Cheyne-Stokes). La transizione verso dinamiche periodiche sono osservabili in molti stati patologici quali il morbo di Parkinson (il tremore), l'apnea notturna ostruttiva, la morte cardiaca improvvisa, l'epilessia, ecc.
L'apparenza paradossale di dinamiche altamente ordinate negli stati patologici (chiamati sul piano medico "disordini") esemplifica il concetto di perdita di complessità nella malattia e nell'invecchiamento. Noi abbiamo definito complessità patologica in relazione, almeno in parte, alla presenza di correlazioni long-range (frattale), insieme con classi distinte di interazioni non lineari. L'antitesi di un sistema senza scale è quello dominato da una frequenza caratteristica. I sistemi fisologici dominati da una sola scala (o poche) mostrano dimaniche altamente periodiche, ripetendo il loro comportamento in un certo lasso di tempo con un pattern altamene predicibile (diremo sindromico).
Mentre i frattali sono irregolari, non tutte le strutture spaziali o temporali sono di tipo frattalico. Un caratteristica chiave per identificare un frattale senbra essere l'ordine su scale temporali o spaziali lunghe. Questa proprietà di correlazione di un oggetto frattale, detta legge di potenza, può essere estesa su molte scale spaziali o temporali dello stesso oggetto in base alla proprietà dell'autosomiglianza. Alcune patologie sono caratterizzate dalla perdita dalla rottura di questa organizzazione, che qualche volta produce una casualità (randomness), detta anche "wtihe noise", distinta dal caos deterministico: esempi sono la risposta erratica ventricolare nella fibrillazione atriale su scale temporali relativamente brevi.
Quindi la rottura della complessità fisiologica frattale (caos deterministico) può configuarsi in due modi:
– eccessivo ordine: periodicità patologica
– eccessivo disordine: casualità (randomness)
Uno degli aspetti che rendono affascinante il caos deterministico è che perturbando un sistema non lineare si possono realizzare effetti parodossali ed imprevisti, a seconda dell'oscillazione del sistema nel momento in cui agisce la causa perturbante.
Le applicazioni in campo odontoiatrico di tali modelli non lineari spiegano ad esempio l'improvvisa insorgenza di un dolore pulpitico, l'improvvisa acutizzazione di una parodontite apicalecuta, ecc.
Anche i batteri e le loro interrelazioni hanno dinamiche non lineari e ciò potrebbe spiegare una serie di fenomeni in endodonzia.
